UNIDAD EDUCATIVA FISCOMICIONAL JAIME ROLDOS  AGUILERA

1.1 Nombre : Estefy Pasochoa

1.2 Curso : 3rO "B"

1.3 Fecha : 06/05/2019

QUE SON LAS FIGURAS CONGRUENTES Y SEMEJANTES

FIGURAS CONGRUENTES

Son aquellas que tienen la misma forma, el mismo tamaño y al superponerlas todos sus puntos coinciden.

Para que dos figuras sean congruentes deben cumplir con las siguientes condiciones:

• Todos sus ángulos interiores correspondientes sean iguales.
• Todos sus lados correspondientes tengan la misma medida.

FIGURAS SEMEJANTES

Son aquellas que tienen la misma forma pero diferente tamaño, es decir, sus lados correspondientes son proporcionales de acuerdo a una razón de semejanza, factor de escala o constante de proporcionalidad.  Cuando dividimos la medida de un lado entre su correspondiente, el número es el mismo es decir es constante en todos los lados de la figura, a este número se le llama razón de semejanza.

Para que dos figuras sean semejantes deben cumplir dos condiciones:

• Sus ángulos correspondientes (homólogos) son iguales.
• Sus lados correspondientes son proporcionales.

CRITERIOS DE CONGRUENCIA Y SEMEJANZA DE TRIÁNGULOS

Al conjunto mínimo de datos que se requieren para asegurar si dos triángulos son CONGRUENTES O SEMEJANTES, se les llama CRITERIOS.

CRITERIOS DE CONGRUENCIA DE TRIÁNGULOS.

Para asegurar que dos triángulos son congruentes, es suficiente que se cumpla cualquiera de los siguientes criterios de congruencia:

• NO. 1. CRITERIO LLL (LADO,LADO,LADO) Los lados correspondientes son iguales. (Congruentes).
• No. 2.- CRITERIO LAL (Lado,ángulo, lado). Los 2 lados correspondientes y elángulo que forman son iguales.
• No. 3.- CRITERIO ALA (Ángulo, lado, ángulo). Dos ángulos   correspondientes  y el lado común son iguales.

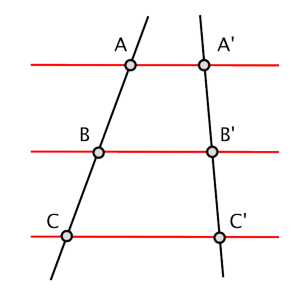
Teorema de Tales

Éste es el teorema básico de las semejanzas.

El Teorema de Tales dice: Si dos rectas, no necesariamente paralelas, son cortadas por un sistema de rectas paralelas, entonces los segmentos que resultan sobre una de las dos rectas son proporcionales a los correspondientes segmentos obtenidos sobre la otra.A continuación, damos una figura para ejemplificar el enunciado anterior:

dónde se cumple que 

Ejemplo

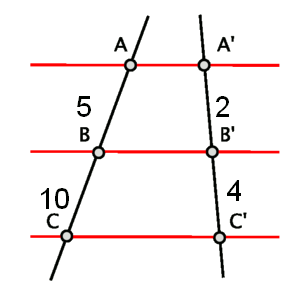
Por ejemplo, dada la figura siguiente, decidir si son o no semejantes los segmentos resultantes.

Como observamos en la figura, las longitudes de los segmentos son los siguientes: ; . Por el Teorema de Tales, se ve que los segmentos de una recta y otra son semejantes gracias a que las razones son iguales:

Para terminar, vamos a dar una aplicación que puede resultar muy útil para la resolución de determinados ejercicios. Gracias al Teorema de Tales, podemos calcular la altura de un objeto, por ejemplo, un árbol, mediante el siguiente mecanismo.

1. Sea  la longitud de la sombra del árbol a una determinada hora.
2. Sea  la longitud de la sombra de un objeto pequeño, por ejemplo un lápiz, en el mismo instante.
3. Sea  la altura del lápiz.