UNIDAD EDUCATIVA FISCOMICIONAL JAIME ROLDOS AGUILERA
1.1 Nombre : Estefy Pasochoa
1.2 Curso : 3rO "B"
1.3 Fecha : 06/05/2019

ESTADÍSTICA

2. MEDIDAS DE TENDENCIA CENTRAL
Al describir grupos de diferentes observaciones, con frecuencia es conveniente resumir la información con un solo número. Este número que, para tal fin, suele situarse hacia el centro de la distribución de datos se denomina medida o parámetro de tendencia central o de centralización.
Cuando se hace referencia únicamente a la posición de estos parámetros dentro de la distribución, independientemente de que esté más o menos centrada, se habla de estas medidas como medidas de posición.1 En este caso se incluyen también los cuantiles entre estas medidas.
Entre las medidas de tendencia central tenemos:

MEDIDAS DE DISPERSIÓN
Medidas de dispersión. Parámetros estadísticos que indican como se alejan los datos respecto de la media aritmética. Sirven como indicador de la variabilidad de los datos. Las medidas de dispersión más utilizadas son el rango, la desviación estándar y la varianza
[
Rango
la dispersión entre los valores extremos de una variable. se calcula como la diferencia entre el mayor y el menor valor de la variable. Se denota como R.
Para datos ordenados se calcula como:
R = x(n) - x(1)
Donde: x(n): Es el mayor valor de la variable. x(n): Es el menor valor de la variable.
Desviación media
Es la media aritmética de los valores absolutos de las diferencias de cada dato respecto a la media.
Donde:
xi:valores de la variable.
n: número total de datos
Desviación estándar
La desviación estándar mide el grado de disersión de los datos con respecto a la media, se denota como s para una muestra o como σ para la población. Se define como la raiz cuadrada de la varianza según la expresión:Obsérvese que el denominador es n - 1, a diferencia de la desviación media donde se divide entre n; también existe la formula de desviación típica donde el denominador es n pero se prefiere n-1.
Varianza
Es otro parámetro utilizado para medir la dispersión de los valores de una variable respecto a la media. Corresponde a la media aritmética de los cuadrados de las desviaciones respecto a la media. Su expresión matemática es:
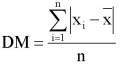
Revisado, 10
ResponderEliminarGracias